機械学習の世界では、モデルの評価や最適化は挑戦的な課題となりますよね。中でも、クロスエントロピーという概念は多くのアルゴリズムで重要な役割を果たしていますが、初めて触れる方にとっては少し難解かもしれません。しかし、心配しないでください!この記事では、クロスエントロピーについて初心者の方でも理解しやすいように解説していきます。さまざまな用語や式をわかりやすく紐解き、機械学習の世界におけるクロスエントロピーの重要性と役割を明確にしていきましょう。
- クロスエントロピーの基本的な概念から具体的な式までの解説
- 情報理論との関連性や、交差エントロピーとの違いについて
- ハイパーパラメータ調整におけるクロスエントロピーの活用方法や、モデルの性能向上に向けた戦略
- 機械学習初心者でもクロスエントロピーについて理解できる
- クロスエントロピーを活用したハイパーパラメータ調整により、モデルの性能向上が可能になる
- 交差エントロピーとの違いを理解し、適切な損失関数の選択に役立てることができる
- 情報理論と機械学習の関連性を知ることで、より深い学習理解が得られる
クロスエントロピーの基本
このセクションでは、クロスエントロピーの基本的な概念について詳しく解説します。
クロスエントロピーとは何か?
クロスエントロピーは、確率分布や予測と真の値の間の差を測る指標であり、機械学習における損失関数として頻繁に使用されます。予測値と真の値が一致する場合、クロスエントロピーは0になります。モデルが正確な予測を行えるように学習する際に、この指標を最小化することが目標となります。
数学的な定義と導出
情報理論の枠組みにおいて、クロスエントロピーは確率分布間の情報量の違いを示す尺度として理解できます。具体的には、真の確率分布\(p\)と予測確率分布\(q\)の間のエントロピーと相対エントロピーを足し合わせたものとして定義されます。
情報理論との関連性
クロスエントロピーは情報理論の重要な概念であり、特に確率分布の比較や情報の圧縮などの分野で活用されます。情報理論は、情報の量や不確実性を定量化するための数学的な枠組みであり、機械学習の中でも重要な基盤となっています。クロスエントロピーは情報理論の観点から、モデルの予測と真の値の間の情報量の違いを計算し、その最小化を通じてモデルの学習を進める際に有用な指標となります。
クロスエントロピーを表す3つの式
\( H(p, q) = -\mathbb{E}_p [\log q] \)
\( H(p, q) = -\sum_{i} p(x_i) \log q(x_i) \)
\( L = -\frac{1}{N}\sum ^{N}_{n=1}t_{n}\log y_{n} \)
クロスエントロピーを表す3つの式について、それぞれの文脈と役割を説明します。
1つ目の式:確率分布によるクロスエントロピー
\( H(p, q) = -\mathbb{E}_p [\log q] \)
この数式は、情報理論における確率分布 \( p \) と \( q \) の間のクロスエントロピーを表現しています。ここで、\( \mathbb{E}_p [\log q] \) は確率分布 \( p \) の下で \( \log q \) の期待値を意味します。この式は、2つの確率分布 \( p \) と \( q \) の間の情報量の違いを示す指標です。情報理論において、クロスエントロピーは確率分布 \( p \) のエントロピーと確率分布 \( q \) の相対エントロピーを足し合わせたものとして定義されます。
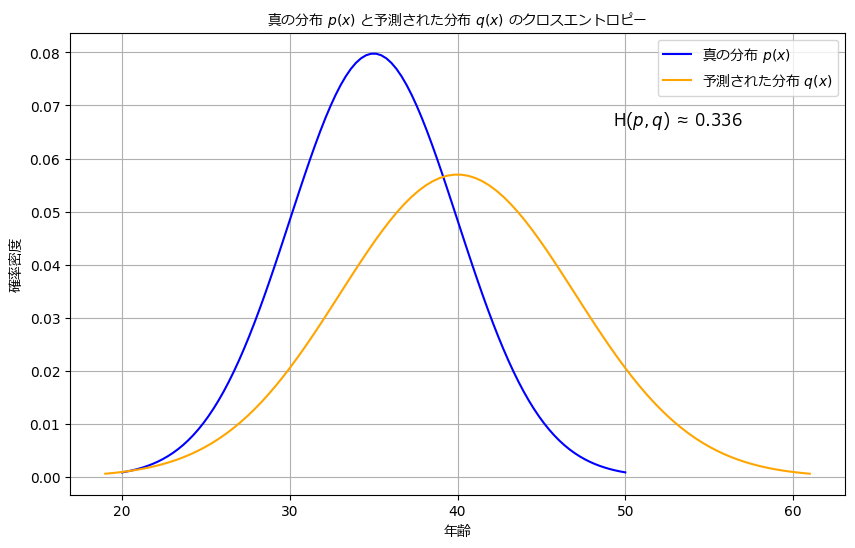
例を交えて説明します。真の年齢分布 \( p \) として、平均年齢が35歳でばらつきがある正規分布を考えます。一方、モデルの予測結果による年齢分布 \( q \) として、平均年齢が40歳でばらつきがある正規分布を仮定します。
クロスエントロピーを計算する手順は以下の通りです:
- 年齢を0歳から100歳まで100点に分割します。この際、連続的な範囲の年齢を等間隔に区切ります。
- 各点における真の年齢分布 \( p \) とモデルの予測結果による年齢分布 \( q \) の確率密度を計算します。これにより、それぞれの点での \( p \) と \( q \) の値を得ます。
- 各点で \( p \) の確率と \( q \) の確率を掛け合わせ、その総和を求めます。この総和は、真の年齢分布 \( p \) の下で \( \log q \) の期待値を表しています。
- 得られた総和を負にしたものがクロスエントロピー \( H(p, q) \) の値になります。このようにすることで、クロスエントロピーの値は常に正の値となります。
この結果から、モデルの予測結果 \( q \) が真の年齢分布 \( p \) から約0.336の情報量の違いがあることが分かります。つまり、モデルがより正確な予測を行うためには、もっと真の年齢分布に近い結果を出す必要があるということがわかります。
以下は上記の例を表すグラフです。
2つ目の式:離散的な確率変数のクロスエントロピー
\( H(p, q) = -\sum_{i} p(x_i) \log q(x_i) \)
2つ目の式も情報理論におけるクロスエントロピーを表していますが、上記の1つ目の式と異なり、連続的な確率変数ではなく離散的な確率変数を扱う場合のクロスエントロピーです。ここでは、\( p(x_i) \) は離散的な確率変数 \( x_i \) の真の確率分布を、\( q(x_i) \) は予測モデルによる確率分布を示しています。各 \( x_i \) の確率を \( \log q(x_i) \) で重み付けして総和を取ることで、確率分布の違いを表すクロスエントロピーが計算されます。
例を交えて説明します。同じ画像分類のタスクを考えますが、ここでは離散的な確率変数 \( x_i \) が「犬」か「猫」の2つのクラスを取る場合を考えます。真の確率分布 \( p \) は、\( x_i \) が「犬」である確率が \( p(\text{犬}) = 1 \)、\( x_i \) が「猫」である確率が \( p(\text{猫}) = 0 \) となります。モデルの出力による確率分布 \( q \) は、\( x_i \) が「犬」である確率が \( q(\text{犬}) = 0.8 \)、\( x_i \) が「猫」である確率が \( q(\text{猫}) = 0.2 \) とします。この場合、2つ目の式は以下のように計算されます:
\( H(p, q) = -\sum_{i} p(x_i) \log q(x_i) = -(1 \cdot \log 0.8 + 0 \cdot \log 0.2) \)
\( H(p, q) = -(0 + 0.223) \)
\( H(p, q) = -0.223 \)
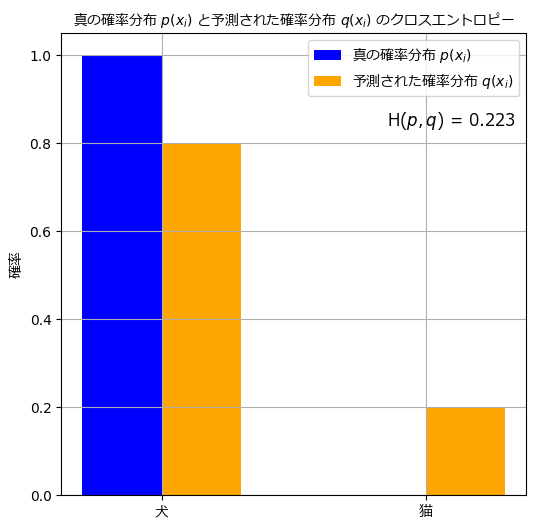
1つ目の式と同様に、この結果から真の確率分布 \( p \) とモデルの出力確率分布 \( q \) の間には約 0.223 の情報量の違いがあることがわかります。
以下は上記の例を表すグラフです。
3つ目の式: クロスエントロピー損失関数
\( L = -\frac{1}{N}\sum ^{N}_{n=1}t_{n}\log y_{n} \)
クロスエントロピー損失の計算を具体的な例を用いて説明します。以下の表に示すデータセットを考えます。
| 画像番号 | 真のラベル (true_labels) | モデルの予測結果 (predicted_probs) |
|---|---|---|
| 1 | 1 (犬) | 0.8 |
| 2 | 0 (猫) | 0.2 |
| 3 | 1 (犬) | 0.6 |
| 4 | 1 (犬) | 0.9 |
| 5 | 0 (猫) | 0.3 |
このデータを用いてクロスエントロピー損失 \( L \) を計算します。
- 各画像のクロスエントロピー損失 \( L_{n} \) を計算します:
\( L_{1} = -1 \cdot \log 0.8 \approx 0.223 \)
\( L_{2} = -0 \cdot \log 0.2 = 0 \)
\( L_{3} = -1 \cdot \log 0.6 \approx 0.511 \)
\( L_{4} = -1 \cdot \log 0.9 \approx 0.105 \) \( L_{5} = -0 \cdot \log 0.3 = 0 \) - データセット中のすべての画像のクロスエントロピー損失 \( L_{n} \) を合計し、平均を取って全体のクロスエントロピー損失 \( L \) を得ます:
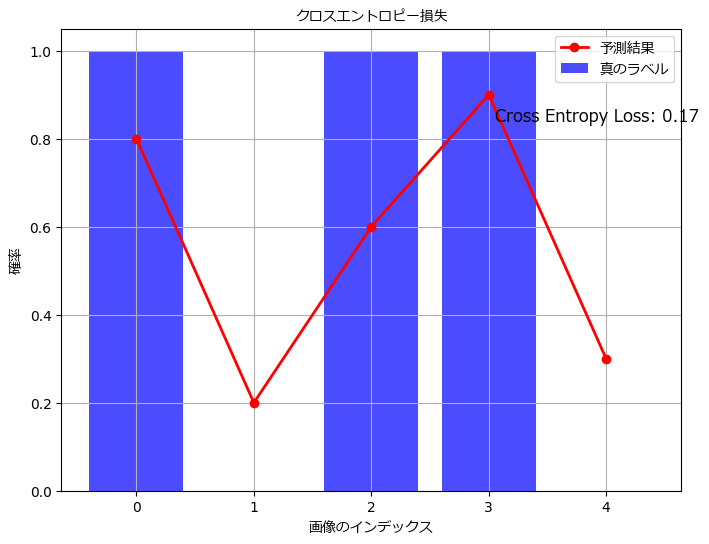
\( L = -\frac{1}{5}(0.223 + 0 + 0.511 + 0.105 + 0) \approx 0.168 \)
このようにして計算されたクロスエントロピー損失 \( L \) は、モデルがデータセット全体に対して平均して約0.168の誤差を持っていることを示しています。モデルの学習においては、このクロスエントロピー損失を最小化するようにモデルのパラメータを調整することが目標となります。損失が小さいほど、モデルの予測結果が真のラベルに近いと言えます。
クロスエントロピー対交差エントロピー
クロスエントロピーと交差エントロピーは、機械学習において似たような概念であり、しばしば混同されることがありますが、それらは微妙に異なる点があります。
交差エントロピーとの違いと比較
クロスエントロピーと交差エントロピーは、共に確率分布の情報量の違いを測る指標であり、モデルの予測と真の値の違いを評価しますが、計算方法や文脈において異なります。
クロスエントロピーは、情報理論の枠組みにおいて確率分布間の情報量を計算する際に使われます。対象とする確率分布 \(p\) と \(q\) の間のエントロピーと相対エントロピーを足し合わせた形で定義されます。一方、交差エントロピーは、主に分類問題における損失関数として用いられます。真のラベルの確率分布 \(p\) とモデルの予測確率分布 \(q\) の間の情報量を計算することで、モデルの予測の精度向上を図るのが主な目的です。
選択基準と最適な使用場面
どちらの指標を使うかは、タスクやモデルの目標によって異なります。クロスエントロピーは情報理論的な観点から情報量の差を測るため、確率分布間の比較やモデルの学習中に用いられます。一方、交差エントロピーは損失関数としてモデルの学習に直接組み込まれるため、主に分類問題において使われます。
最適な使用場面を選択するには、具体的な問題の性質やデータの特徴、モデルのアーキテクチャなどを考慮する必要があります。大抵の場合、両者は似たような結果をもたらすことが多いため、どちらを選んでも問題ないケースもありますが、専門的なコンテキストでは適切な指標の選択が重要です。また、実践においては両者の組み合わせや他の損失関数との比較も行い、より高い性能を得るための工夫が行われることがあります。
クロスエントロピーを活用したハイパーパラメータ調整
ハイパーパラメータ調整は、機械学習モデルの性能を向上させるために重要な手法です。ハイパーパラメータは、モデルの学習に関わる設定値であり、例えば学習率、バッチサイズ、隠れ層のユニット数などが含まれます。これらのハイパーパラメータの選択が、モデルの性能や学習の収束に大きな影響を与えるため、適切な調整が必要です。
ハイパーパラメータ最適化手法とクロスエントロピーとの関係
クロスエントロピーを活用したハイパーパラメータ調整では、モデルの性能を最適化するためにクロスエントロピー損失を用いてハイパーパラメータの評価を行います。一般的な手法として、以下のようなアプローチが考えられます。
- グリッドサーチ (Grid Search)
ハイパーパラメータの値を事前に定義した範囲内で全ての組み合わせを試す手法です。例えば、学習率や隠れ層のユニット数などの値をあらかじめリスト化し、全ての組み合わせでモデルを学習し、クロスエントロピー損失を評価します。最も性能の良い組み合わせを選択します。ただし、計算コストが高いため、ハイパーパラメータの候補数が多い場合には適していません。 - ランダムサーチ (Random Search)
グリッドサーチの代わりに、ハイパーパラメータをランダムに選択する手法です。ランダムにサンプリングされた値でモデルを学習し、クロスエントロピー損失を評価します。この方法はグリッドサーチよりも計算コストが少なく、効率的にハイパーパラメータの最適な組み合わせを探索することができます。 - ベイズ最適化 (Bayesian Optimization)
ハイパーパラメータの最適化にベイズ最適化を適用する手法です。これは、過去のハイパーパラメータの評価結果を用いて、次に評価すべきハイパーパラメータの値を確率的に推定する方法です。これにより、効率的に最適なハイパーパラメータを見つけることができます。クロスエントロピー損失を評価する際に、ベイズ最適化を用いてハイパーパラメータ探索を行います。
モデルの性能向上に向けた戦略
ハイパーパラメータ調整においては、クロスエントロピー損失を用いた評価が重要ですが、その他の戦略もモデルの性能向上に役立ちます。例えば、データの前処理や特徴量の選択、モデルのアーキテクチャの改良、データ拡張なども考慮すべきです。クロスエントロピーを用いたハイパーパラメータ調整は、モデルの学習の初期段階から行われるべき重要なステップですが、総合的なアプローチでモデルの性能を向上させるためには、これらの戦略を組み合わせることが必要です。
おわりに
クロスエントロピーは機械学習や情報理論で重要な概念です。この記事では、3つの式によってクロスエントロピーを表現し、その意味や役割について説明しました。1つ目の式は確率分布の情報量を示し、2つ目の式は離散的な確率変数を扱う場合のクロスエントロピーを表します。3つ目の式は機械学習におけるクロスエントロピー損失関数であり、モデルの学習に利用されます。クロスエントロピーはモデルの予測と真のラベルの違いを評価する重要な指標であり、より正確な予測を行うために最適なパラメータを調整する役割を果たします。これらの知識を活用して、機械学習の理解と実践に役立ててください。



コメント