ディープラーニングで活用される活性化関数について疑問を持ったことはありませんか?活性化関数はなぜ非線形である必要があるのでしょうか?この記事では、活性化関数の役割と代表的な種類についてわかりやすく説明します。
- 活性化関数の基本的な概念
- シグモイド関数、ReLU関数、tanh関数などの具体的な活性化関数についての理解
- 各活性化関数の特性、利点、課題に関する詳細な説明
- 活性化関数の選択がニューラルネットワークの性能に与える影響についての紹介
- 活性化関数の重要性と役割が理解できる
- シグモイド関数、ReLU関数、tanh関数の違いを把握できる
- 勾配消失問題や勾配飽和問題の理解が深まる
- 活性化関数の選択がネットワークの学習に与える影響を理解できる
- 最新の深層学習の活性化関数に関する知識が身につく
1. 活性化関数とは何か?
活性化関数は、ニューラルネットワークの重要な構成要素であり、ニューロンの出力を非線形に変換する関数です。ニューラルネットワークは、入力データを受け取り、それを次の層に伝える際に、各ニューロンの出力を計算します。このとき、活性化関数がその出力を変換する役割を果たします。
活性化関数は非線形である必要があります。なぜなら、もし活性化関数が線形だと、ニューラルネットワークの隠れ層を何層にしても、結局は単一の線形変換になってしまい、複雑な関数を表現できなくなるからです。
2. パーセプトロンとステップ関数
パーセプトロンは、1950年代にフランク・ローゼンブラットによって提案された単純なニューラルネットワークモデルです。パーセプトロンは、複数の入力 \(x\) に対して重み付き和を計算し、その結果に閾値を適用して0または1の2値の出力を行います。この出力にはステップ関数が使われることが一般的でした。
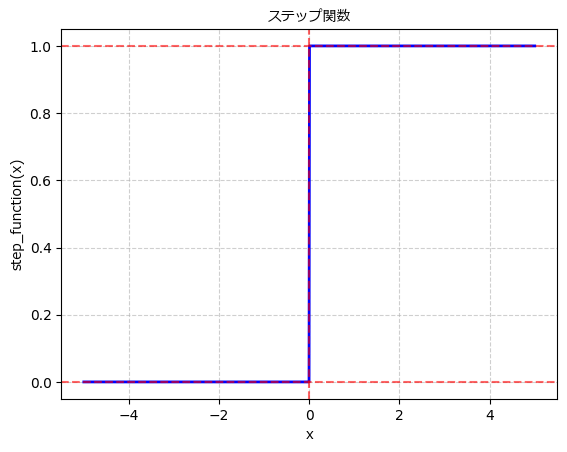
ステップ関数は、入力が閾値を超えたら1を出力し、それ以外は0を出力する非常に単純な活性化関数です。しかし、ステップ関数は微分不可能であり、勾配降下法などの学習アルゴリズムに適用することができません。このため、ステップ関数は現在では主に歴史的な観点から扱われることが多くなっています。
3. シグモイド関数
シグモイド関数は、ニューラルネットワークにおいて最も古くから使われてきた活性化関数の一つです。シグモイド関数は次のような数式で表されます:
$$
f(x) = \frac{1}{1 + e^{-x}}
$$
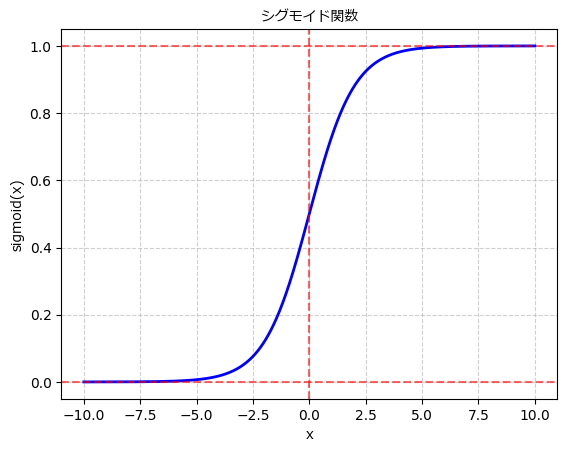
この関数は入力を0から1の範囲に変換します。入力が大きい場合は1に近づき、小さい場合は0に近づきます。この性質により、シグモイド関数は入力を確率のように解釈することができ、特に2クラス分類問題に適しています。
しかし、シグモイド関数は勾配飽和問題と呼ばれる課題があります。入力が非常に大きな正または負の値を取ると、その微分値が0に近づいてしまい、勾配消失問題が発生します。勾配消失問題により、学習が非常に遅くなったり、学習が進まなくなることがあります。また、シグモイド関数は原点を中心として非対称な形状を持ちます。
4. ReLU関数
ReLU関数(Rectified Linear Unit)は、近年のディープラーニングにおいて広く使われている活性化関数です。ReLU関数は次のような数式で表されます:
$$
f(x) = \max(0, x)
$$
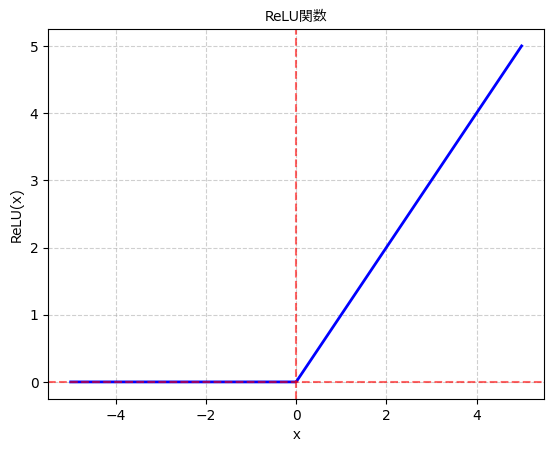
入力が正の値の場合はそのままの値を出力し、負の値の場合は0を出力します。ReLU関数は計算が非常に高速であり、勾配消失問題を緩和する効果があります。また、ReLU関数は原点対称ではなく、入力が正の領域では線形になるため、ネットワークがより複雑な関数を学習できる特性があります。
ただし、ReLU関数にも「死のReLU(dying ReLU)」問題と呼ばれる課題が存在します。入力が負の値の場合、その出力は常に0となり、勾配が0になります。このため、学習中に一部のニューロンが非活性化してしまい、情報の欠落が生じる可能性があります。
5. tanh関数
tanh関数(Hyperbolic tangent function関数)は、シグモイド関数を拡大縮小させた関数です。tanh関数は次のような数式で表されます:
$$
f(x) = \frac{{e^x – e^{-x}}}{{e^x + e^{-x}}}
$$
tanh関数は入力を-1から1の範囲に変換します。シグモイド関数と似た形状を持ちますが、原点対称になっています。tanh関数はシグモイド関数と同様に非線形な性質を持ち、勾配消失問題への対処に一定の効果があります。
しかし、tanh関数もシグモイド関数と同様に勾配飽和問題が存在します。入力が大きな値を取
ると、その微分値が0に近づき、学習が進まなくなる可能性があります。それでもシグモイド関数よりも範囲が広いため、情報の表現力は高くなります。
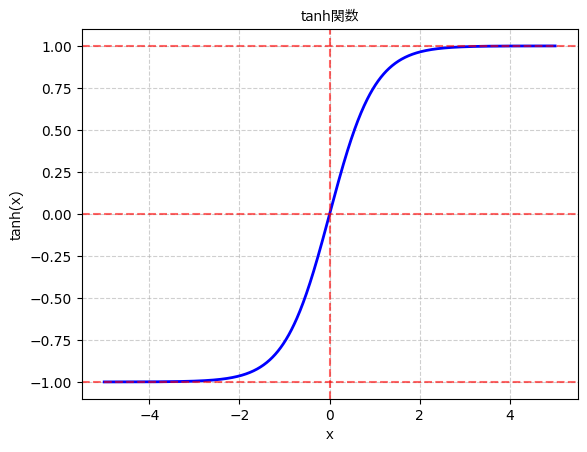
シグモイド関数とtanh関数の比較


まとめ
活性化関数はニューラルネットワークにおいて重要な役割を果たす非線形な関数です。ニューロンの出力を非線形に変換することにより、複雑な関数を近似し、より高度な問題を解決できるようになります。
- 活性化関数は非線形である必要があります。線形関数を使うと、隠れ層を重ねても結局は線形変換になり、複雑な関数を表現できません。
- パーセプトロンは古典的なニューラルネットワークモデルであり、ステップ関数を活性化関数として使っていました。しかし、ステップ関数は微分不可能で学習に向いていません。
- シグモイド関数は昔から使われている活性化関数で、入力を0から1の範囲に変換します。ただし、勾配消失問題や勾配飽和問題がある点に注意が必要です。
- ReLU関数は近年よく使われる活性化関数で、特に勾配消失問題を軽減する効果があります。しかし、一部のニューロンが非活性化する「死のReLU」問題に対処する必要があります。
- tanh関数はシグモイド関数を拡大縮小させた関数で、-1から1の範囲に変換します。勾配消失問題への対処に一定の効果がありますが、勾配飽和問題も考慮すべき点です。
これらの活性化関数を理解し、適切に選択することで、より効果的なニューラルネットワークを構築できます。AIエンジニアを目指す皆さんには、活性化関数の重要性を理解し、ディープラーニングの学習に役立てていただければ幸いです。頑張ってください!


コメント